Double DQN :
Deep Deterministic Policy Gradient (DDPG):
Continuous DQN (CDQN or NAF):
Dueling network DQN (Dueling DQN) :
Dueling Network Architectures for Deep Reinforcement Learning
Deep SARSA : [10]
Asynchronous Advantage Actor-Critic (A3C) :
Proximal Policy Optimization Algorithms (PPO):
Cross-Entropy Method(CEM):
1. Double DQN
Q值函数的定义:
在策略π下,状态s,采取动作a, 所得到的Q值为:

最优值就是:
最优策略就可以通过在每个状态选择最高值的行动给出。
则目标

DQN 算法
DQN 算法的两个最重要的特点是目标网络 (target network) 和经验回顾 (experience replay)。目标网络,其参数为 θ^-,和 online的网络一样,除了其参数是从 online network 经过某些steps之后拷贝下来的。
目标网络是:

Double Q:
在标准的 Q-学习和 DQN 中的 max 操作用相同的值来选择和评价一个 action,这实际上更可能选择过高的估计值,从而导致过于乐观的值估计overestimated values。为了避免这种情况的出现,我们可以对选择selection 和衡量evaluation进行解耦。这就是 Double Q。
reference: Double DQN
Background
论文(Hasselt等人)发现并证明了传统的DQN普遍会过高估计Action的Q值,而且估计误差会随Action的个数增加而增加。如果高估不是均匀的,则会导致某个次优的Action高估的Q值超过了最优Action的Q值,永远无法找到最优的策略。作者在他2010年提出的Double Q-Learning的基础上,将该方法引入了DQN中。具体操作是对要学习的Target Q值生成方式进行修改,原版的DQN中是使用TargetNet产生Target Q值,即
其中$θ^-$是TargetNet的参数。
Steps
在DDQN中,先用MainNet找到 $\max{a’}Q(s’,a’;\theta{i})$的Action ($θ_i$是MainNet的参数)
再去TargetNet中找到这个Action的Q值来去构成Target Q值,这个Q值在TargetNet中不一定是最大的,因此可以避免选到被高估的次优Action。最终要学习的Loss Function为:
此时的Target Q 变为:
除此之外,其他设置与DQN一致。实验表明,DDQN能够估计出更准确出Q值,在一些Atari2600游戏中可获得更稳定有效的策略。
reference: Doule DQN
2. Dueling-DQN
Background
Wang等人提出了一种竞争网络结构(dueling network)作为DQN的网络模型。
Structure
第一个模型是一般的DQN网络模型,即输入层接三个卷积层后,接两个全连接层,输出为每个动作的Q值。
第二个模型—竞争网络(dueling net)将卷积层提取的抽象特征分流到两个支路中:
- 上路代表状态值函数 $V(s)$,表示静态的状态环境本身具有的价值
- 下路代表依赖状态的动作优势函数$A(a)$(advantage function),表示选择某个Action额外带来的价值。
最后这两路再聚合再一起得到每个动作的Q值。
论文作者认为,V(s)更专注于环境,A(a)更专注与动作本身对结果的影响,以车的游戏做了举例说明
公式
状态价值函数表示为
动作优势函数表示为
动作Q值为两者相加
其中 θ 是卷积层参数,β 和 α 是两支路全连接层参数。而在实际中,一般要将动作优势流设置为单独动作优势函数减去某状态下所有动作优势函数的平均值
这样做可以保证该状态下各动作的优势函数相对排序不变,而且可以缩小 Q 值的范围,去除多余的自由度,提高算法稳定性。reference:Dueling-DQN
3. Prioritized Experience Replay
简单来说,经验池中TD误差 绝对值越大的样本被抽取出来训练的概率越大,加快了最优策略的学习。
4. H-DQN
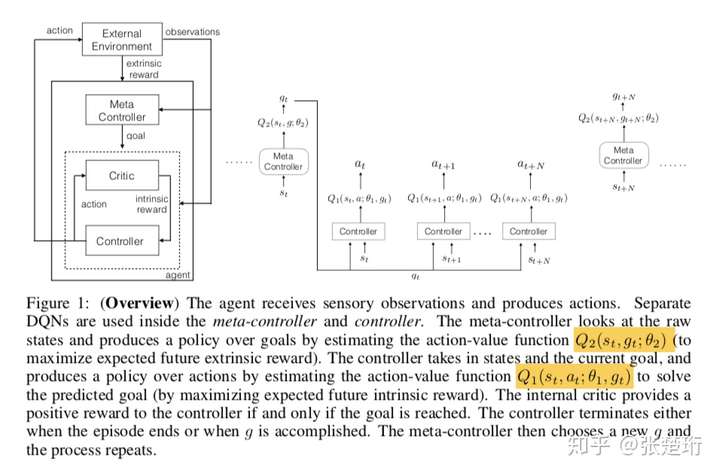
Introduction
hierarchical deep reinforcement learning, model-free, value-based
当环境反馈是sparse和delayed时,解决方法是构造一个两个层级的算法,将困难问题分解为多个小目标,逐个完成。
Procedure
以一个两层级的算法为例:
- 一个层级叫做meta-controller,它负责获取当前状态$st$ ,然后从可能的子任务里面选取一个子任务 g_t \in \mathcal{G} 交代给下一个层级的控制器去完成。它是一个强化学习算法,其目标是最大化实际得到的extrinsic reward之和,$F_t = \sum{t’=t}^\infty \gamma^{t’-t} f_{t’}$ 。
在这里,这一层使用的是DQN方法,这一层Q-value的更新目标是:
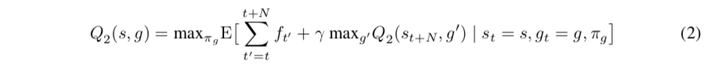
ps: 按照sih的理解,通俗来讲就是,状态s和作为该层级的动作->子任务$g$,以及外置奖励(此处的外置奖励来源于外部环境)进行一次DQN的学习。
- 另一个层级叫做controller,它负责接收上一个层级的子任务 $g$ 以及当前的状态 $st$ ,然后选择一个可能的行动 $a_t$ 去执行。它也是一个强化学习算法,其目标是最大化一个人为规定的critic给出的intrinsic reward之和,$R_t(g) = \sum{t’=t}^\infty \gamma^{t’-t} r_{t’}(g)$。这里也使用DQN方法,更新目标为:
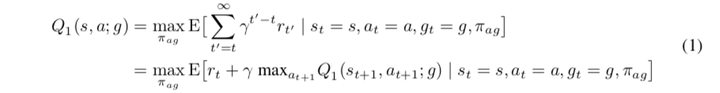
ps: 此步则是以上一层级的子任务g作为先验,将s,a,g,以及内置奖励(此处的内置奖励来源于critic)进行DQN的学习。
算法框架